

登神长阶
第五神装 二叉树 Binary-Tree
目录
?一.树形结构
?1.概念
?2.具体应用
? 二.二叉树(Binary Tree)
?1.概念
?2.表现形式
?3.特殊类型
?3.1完全二叉树(Complete Binary Tree)
?3.2满二叉树(Full Binary Tree)
?4.性质
?5.二叉树的遍历
?5.1前中后序遍历
? 5.2层序遍历
? 三.总结与反思
?一.树形结构
?1.概念
树形结构是一种在Java中常见的数据结构,它由节点(node)组成,这些节点之间以分支(branch)相连的方式形成层次关系。树形结构中通常包含一个根节点(root node),以及每个节点可能有零个或多个子节点(child nodes)。每个节点可以有一个父节点(parent node),除了根节点,它没有父节点。
在Java中,树形结构通常通过类和对象来表示。每个节点可以是一个类的实例,这个类通常包含一个指向父节点的引用和一个指向子节点的引用。通过这些引用,可以在树形结构中导航和操作节点。
树形结构在计算机科学中有广泛的应用,例如在文件系统中用于表示文件和文件夹的层次结构,在数据库中用于表示层次化数据,以及在图形用户界面(GUI)中用于构建菜单和组织UI元素等。

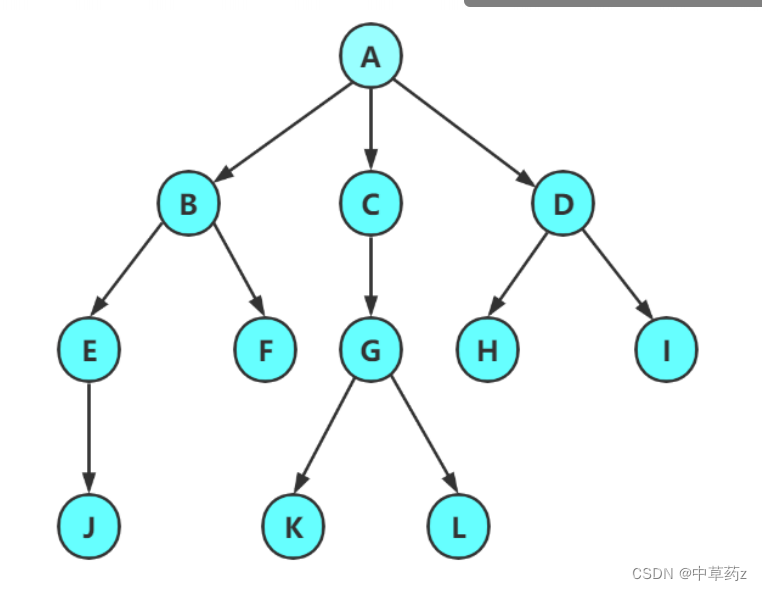
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
?2.具体应用
树形结构在计算机科学和软件工程中有着广泛的应用,以下是一些常见的应用场景:
文件系统
文件系统通常以树形结构的形式来组织文件和目录,每个目录可以包含零个或多个子目录和文件,形成层次化的结构。这种结构使得用户可以方便地组织和管理文件。数据库
在数据库中,树形结构常用于表示层次化数据,例如组织结构、产品分类、论坛板块等。通过树形结构,可以方便地进行数据检索、添加、删除和更新操作,同时保持数据的层次关系。图形用户界面(GUI)
GUI 应用程序中经常使用树形结构来构建菜单、导航栏和组织 UI 元素。例如,文件资源管理器中的目录树、网站导航菜单等都是树形结构的应用。编程语言中的抽象语法树(AST)
在编译器和解释器中,树形结构被用来表示源代码的抽象语法结构。抽象语法树(AST)将源代码表示为树的形式,每个节点代表源代码中的一个语法结构,如表达式、语句、函数等,方便进行语法分析和程序转换。网络路由与拓扑排序
在网络领域,树形结构可以用于路由算法的实现,例如通过构建路由表来确定数据包的传输路径。此外,在计算机网络的拓扑结构中,也可以使用树形结构来表示网络节点之间的关系,进行拓扑排序和数据传输优化。树形结构的应用不仅局限于以上几个领域,还涵盖了许多其他领域,如人工智能、游戏开发、数据可视化等。其灵活性和可扩展性使得树形结构成为解决各种复杂问题的有力工具。
? 二.二叉树(Binary Tree)
?1.概念

二叉树是树形结构中最常见的一种,具有以下基本概念:
结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为6 树的度:一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为6 叶子结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I...等节点为叶结点 双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点 根结点:一棵树中,没有双亲结点的结点;如上图:A 结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推树的高度或深度:树中结点的最大层次; 如上图:树的高度为4 树的以下概念只需了解,在看书时只要知道是什么意思即可: 非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G...等节点为分支结点 兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点 堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点 结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先 子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙 森林:由m(m>=0)棵互不相交的树组成的集合称为森林?2.表现形式
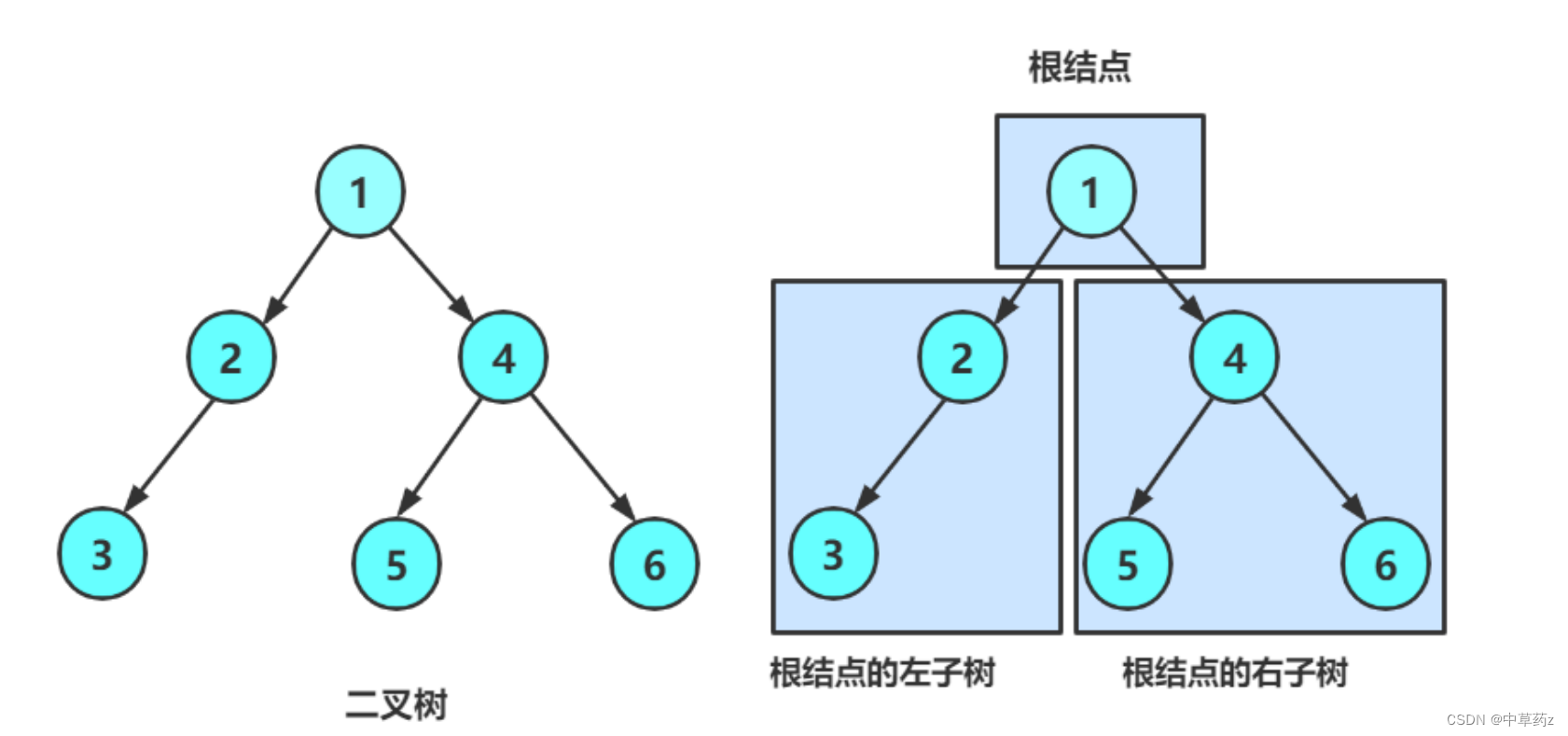
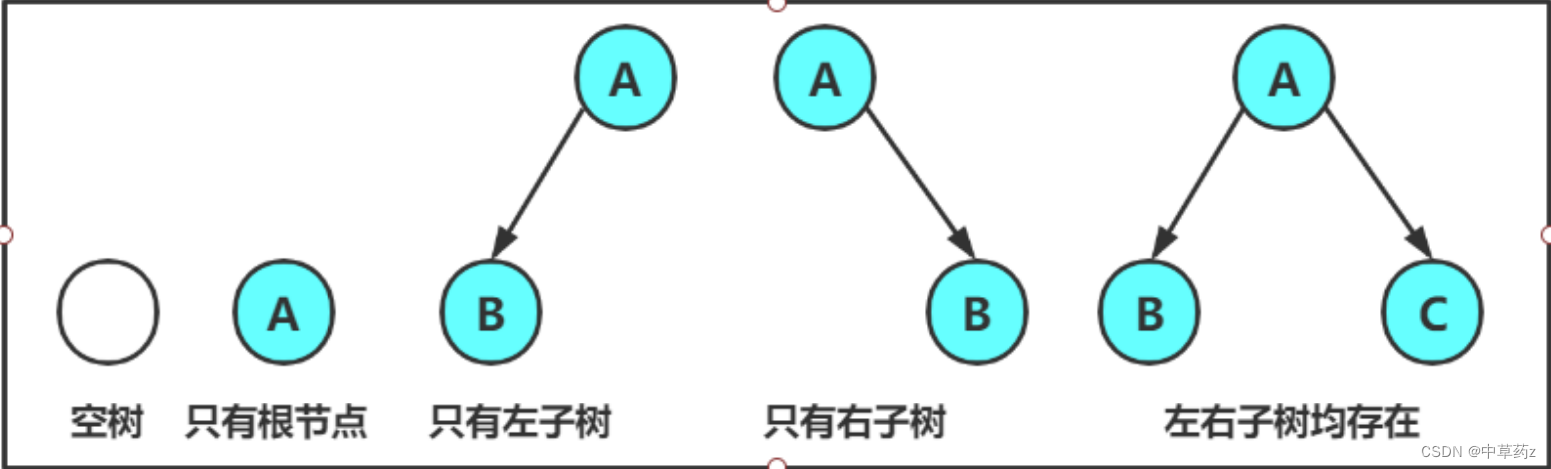
class TreeNode { public char val; public TreeNode left;//左孩子的引用 public TreeNode right;//右孩子的引用 public TreeNode(char val) { this.val = val; } }?3.特殊类型
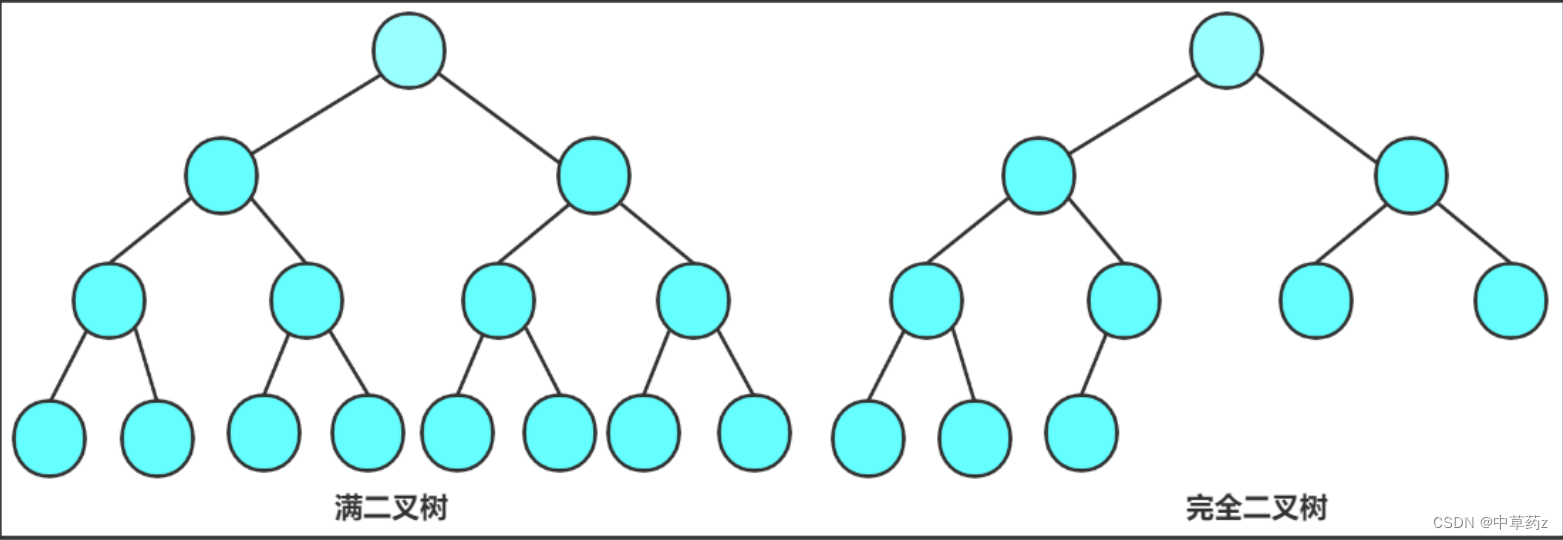
?3.1完全二叉树(Complete Binary Tree)
完全二叉树是指除了最后一层外,其他每一层都被完全填满,并且最后一层的节点都依次从左向右排布,不留有空缺的二叉树。在完全二叉树中,如果某个节点没有右子节点,则它一定没有左子节点。
性质:
完全二叉树的高度为 h,节点数目在 [2^(h-1), 2^h - 1] 的范围内。如果将完全二叉树按照从上到下、从左到右的顺序对节点进行编号,那么对于任意一个节点 i,其左子节点的编号为 2i,右子节点的编号为 2i + 1,父节点的编号为 i/2(当 i 不为根节点时)。完全二叉树的叶子节点一定集中在最底层和次底层,且最底层的叶子节点依次从左到右排布。示例:
下图展示了一个完全二叉树的示例:
1 / \ 2 3 / \ 4 5 在这个示例中,该完全二叉树的高度为 3,共有 5 个节点。
?3.2满二叉树(Full Binary Tree)
满二叉树是一种特殊的二叉树,每个节点要么是叶子节点,要么具有两个子节点。满二叉树的所有非叶子节点都有两个子节点,且所有叶子节点都在同一层上。
性质:
满二叉树的高度为 h,节点数目为 (2^h - 1)。满二叉树的叶子节点数目等于 (2^(h-1))。满二叉树中任意节点的度为 0 或 2。示例:
下图展示了一个满二叉树的示例:
1 / \ 2 3 / \ / \ 4 5 6 7在这个示例中,该满二叉树的高度为 3,共有 (2^3 - 1 = 7) 个节点,所有叶子节点都在第三层上。
满二叉树是一种特殊的完全二叉树
?4.性质
若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有2^i-1(i>0)个结点 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是 2^k-1(k>=0) 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1 具有n个结点的完全二叉树的深度k为log2(n+1)上取整 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有: 若i>0,双亲序号: (i-1)/2 ; i=0 , i 为根结点编号,无双亲结点 若2i+1<n,左孩子序号: 2i+1,否则无左孩子 若2i+2<n,右孩子序号: 2i+2,否则无右孩子?5.二叉树的遍历
?5.1前中后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓遍历 (Traversal) 是指沿着某条搜索路线,依次对树中每个结 点均做一次且仅做一次访问 。 访问结点所做的操作依赖于具体的应用问题 ( 比如:打印节点内容、节点内容加1)。 遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础。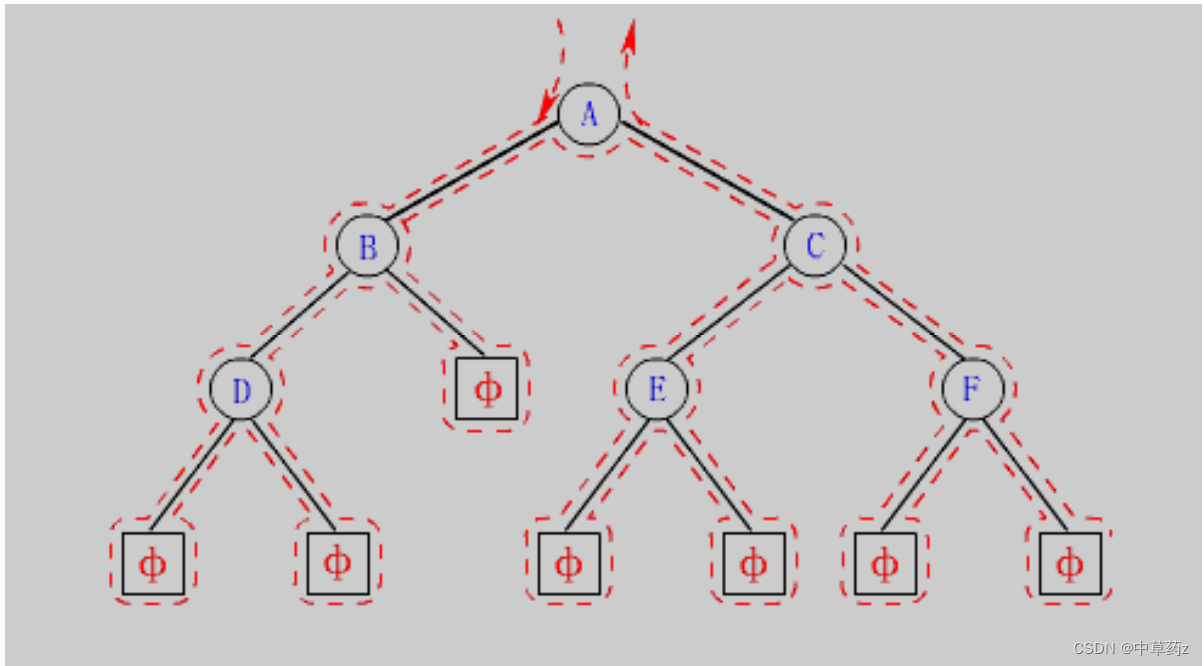
在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱, 如果按 照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的 。如果 N 代表根节点, L 代表根节点的左子树,R 代表根节点的右子树,则根据遍历根节点的先后次序有以下遍历方式: NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。 LNR:中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。 LRN:后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。
以下我们用递归方式,来实现这三种遍历方式,逻辑非常简单,以前序遍历举例:

代码如下:
// 前序遍历 public void preOrder(TreeNode root) { if (root==null){ return; } System.out.print(root.val+" "); preOrder(root.left); preOrder(root.right); } // 中序遍历 void inOrder(TreeNode root) { if (root==null){ return; } inOrder(root.left); System.out.print(root.val+" "); inOrder(root.right); } // 后序遍历 void postOrder(TreeNode root) { if (root==null){ return; } postOrder(root.left); postOrder(root.right); System.out.print(root.val+" "); }? 5.2层序遍历
设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。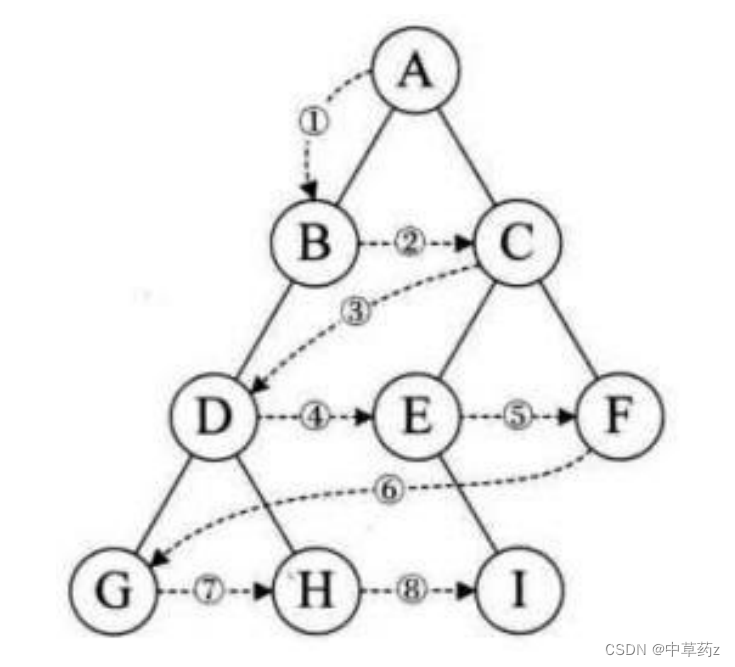
首先检查根节点是否为空,然后创建一个队列来存储待处理的节点。在遍历过程中,每次从队列中取出当前层的所有节点,并将它们的值添加到当前层的列表中。然后将每个节点的子节点(如果存在)加入队列,以便遍历下一层。最后将当前层的列表添加到结果列表中,直到队列为空,遍历完成。
import java.util.*;// 二叉树节点类class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; }}public class LevelOrderTraversal { //返回List<List<Integer>> public List<List<Integer>> levelOrder1(TreeNode root) { List<List<Integer>> result = new ArrayList<>(); if (root == null) return result; Queue<TreeNode> queue = new LinkedList<>(); queue.offer(root); while (!queue.isEmpty()) { int levelSize = queue.size(); // 当前层的节点数 List<Integer> currentLevel = new ArrayList<>(); // 遍历当前层的所有节点 for (int i = 0; i < levelSize; i++) { TreeNode node = queue.poll(); currentLevel.add(node.val); // 将当前节点的值加入当前层列表 // 将当前节点的子节点加入队列,用于遍历下一层 if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } result.add(currentLevel); // 将当前层的列表加入结果列表 } return result; } //直接打印 public void levelOrder2(TreeNode root) { Queue<TreeNode> queue=new LinkedList<>(); if (root==null){ return; } queue.offer(root); while(!queue.isEmpty()){ TreeNode cur=queue.poll(); System.out.print(cur.val+" "); if (cur.left!=null){ queue.offer(cur.left); } if (cur.right!=null){ queue.offer(cur.right); } } System.out.println(""); }}? 三.总结与反思
漫长的岁月既毁坏了坟墓又损坏了墓碑可是光阴对于书却无能为力。——瓦鲁阿
学习了Java中二叉树的过程让我受益匪浅。首先,我意识到了数据结构在编程中的关键性,二叉树作为其中的重要一环,对算法设计和问题解决都有着深远的影响。深入理解二叉树的基本概念,如节点、根节点、子节点等,为我理解二叉树结构和算法打下了坚实的基础。掌握了常见的操作和遍历算法,如插入节点、删除节点以及深度优先遍历和广度优先遍历,这些都是对树形结构理解和应用至关重要的。
通过编写Java代码实现二叉树的操作和算法,我不仅加深了对二叉树的理解,也提升了编程能力。在未来,我希望能更深入地理解算法原理,探索二叉树在不同应用场景中的多样化应用,并持续学习与实践,以不断提升自己的编程能力和解决问题的能力。
????????????????????????????
以上,就是本期的全部内容啦,若有错误疏忽希望各位大佬及时指出?
制作不易,希望能对各位提供微小的帮助,可否留下你免费的赞呢?