目录
一.基本理论
二.两类相关系数的对比
三.相关系数的假设检验
四.MATLAB的相关操作
五.其他有关的一些列技巧
六.案例展示
七.实战操作
一.基本理论
所谓相关系数,本质上是来衡量两组数据的关系大小——对应呈现函数关心的两种变量,那么我们可以很清楚他们之间的关系;而对于没有强烈关联的变量,我们若无法抽象他们之间的函数,那么可以用相关性强弱来描述他们之间的关系所在。


如上是有关相关系数的计算方式:所谓的皮尔逊相关系数,即为我们本科期间学过的那种,也就是考研数一数三会涉及的部分~

如下是需要注意的一些列理论知识: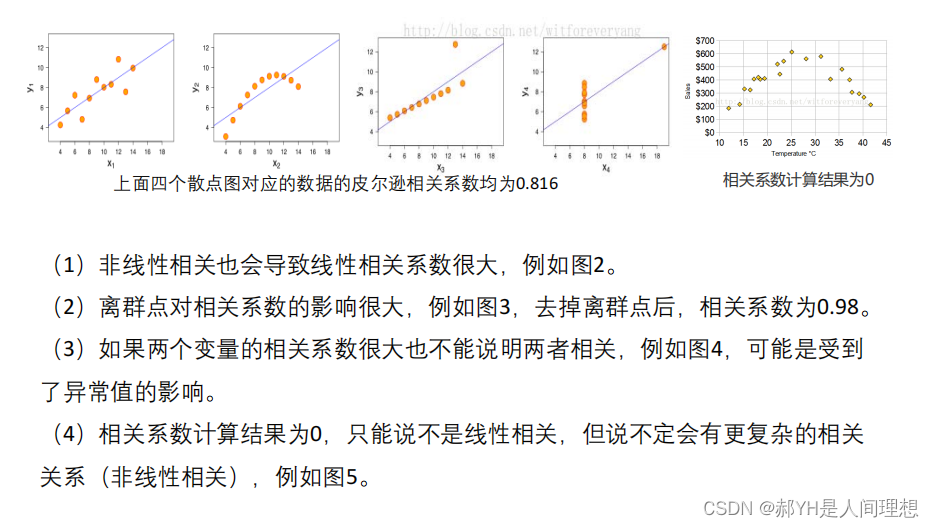 总的来说,当变量之间呈现线性关系时,才有考虑相关系数大小的意义~
总的来说,当变量之间呈现线性关系时,才有考虑相关系数大小的意义~

如上是衡量相关性强弱的普遍标准:一般认为相关系数大于0.5时,呈现较强的相关性~
二.两类相关系数的对比
通常我们会接触到皮尔逊相关系数和斯皮尔曼相关系数两种类型。
如下是关于斯皮尔曼相关系数的理论:
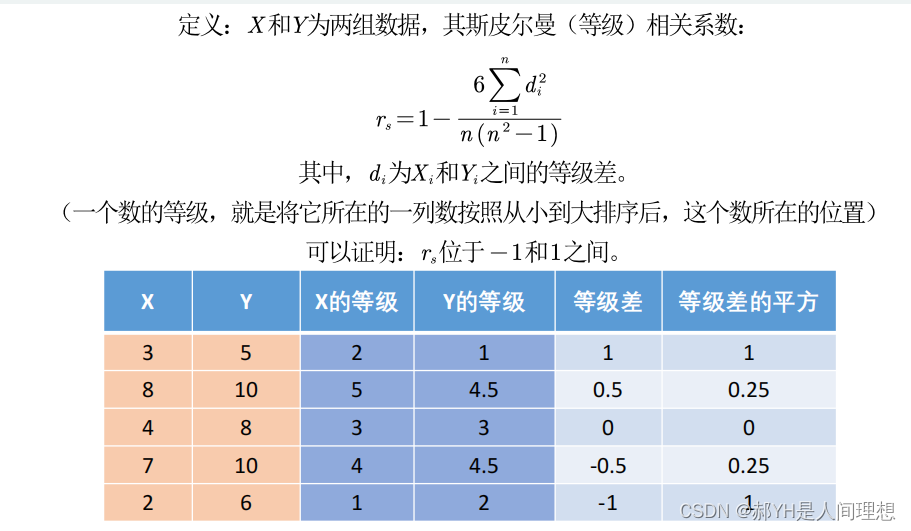
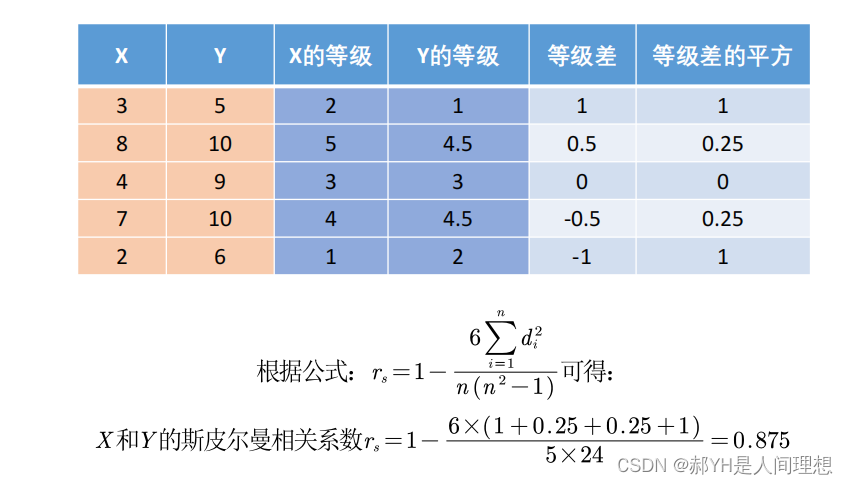 如下是区别方式:
如下是区别方式:

三.相关系数的假设检验
这一部分非常理论,考数一的同学可以稍微研究研究,不过还是以实际操作为重点~

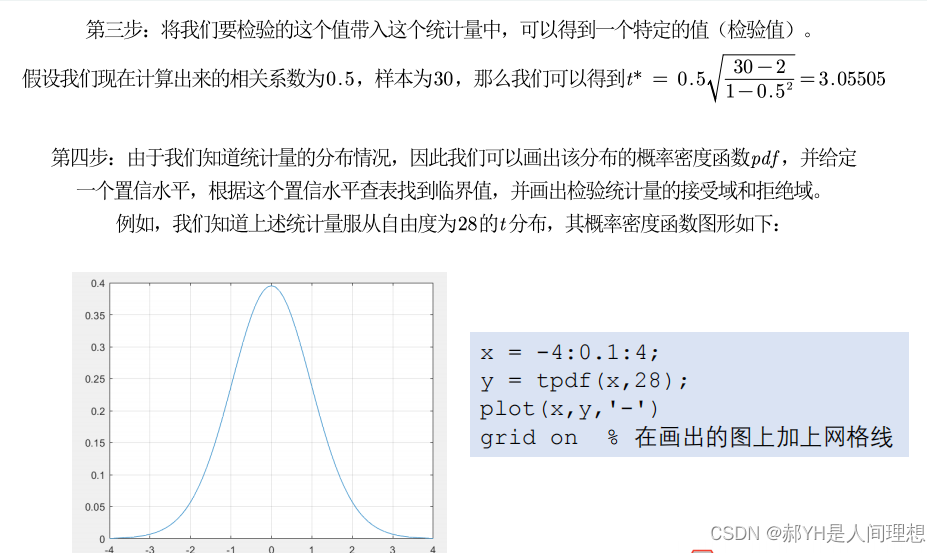
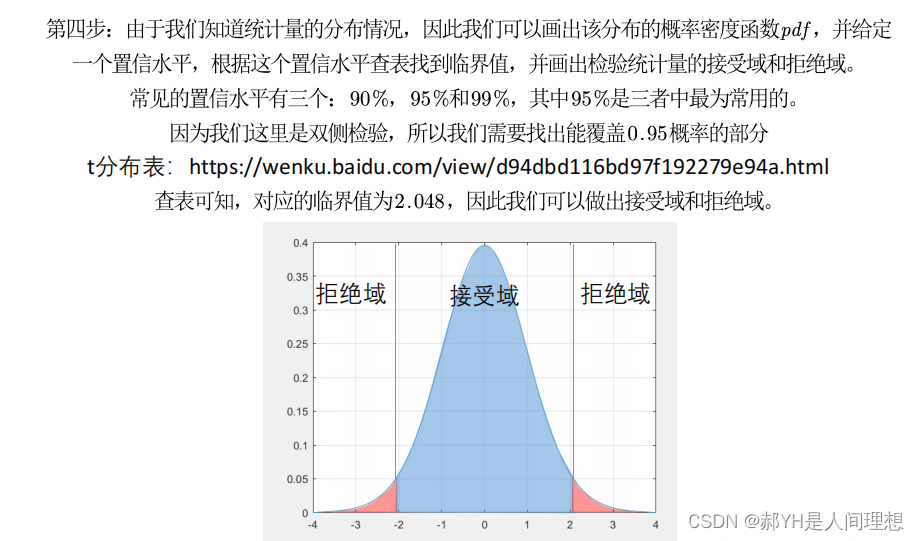
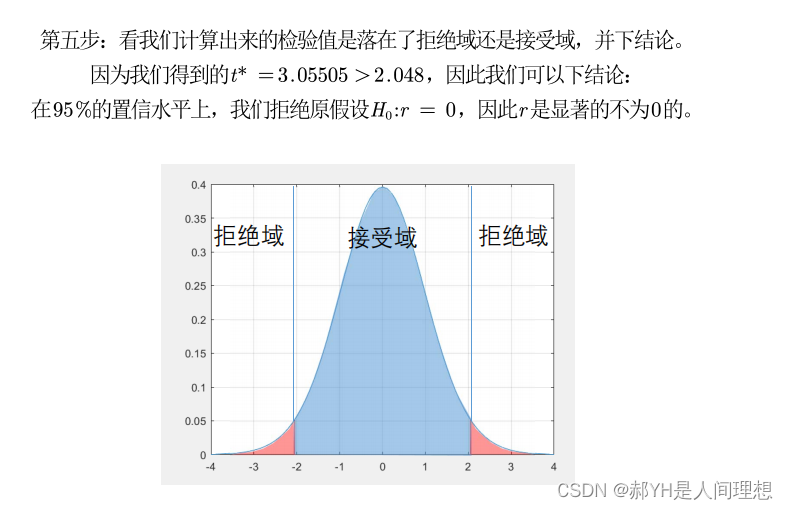
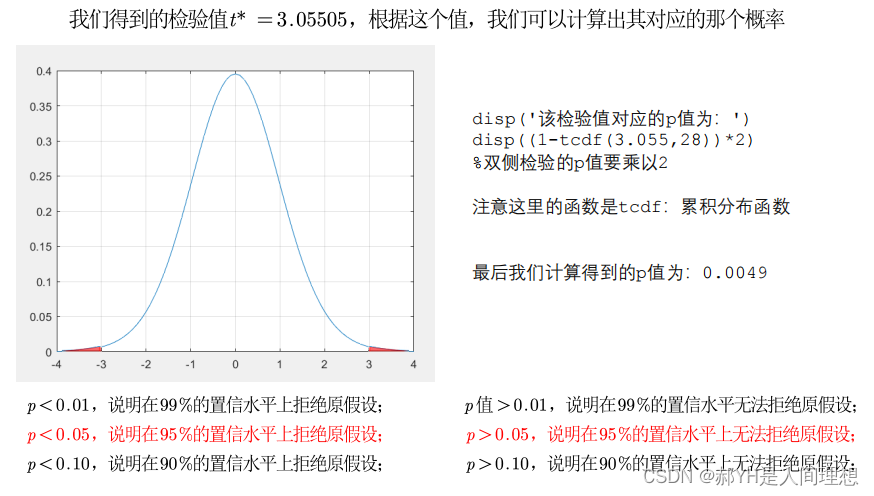
满足假设检验的条件:
第一, 实验数据通常假设是成对的来自于正态分布的总体。 因为我们在求皮尔 逊相关性系数以后,通常还会用 t 检验之类的方法来进行皮尔逊相关性系数检验, 而 t 检验是基于数据呈正态分布的假设的。 第二, 实验数据之间的差距不能太大。 皮尔逊相关性系数受异常值的影响比较 大。 第三:每组样本之间是独立抽样的。 构造 t 统计量时需要用到。
四.MATLAB的相关操作
如下是20个初二学生的身高及跳远成绩:
| 身高 | 立定跳远 |
| 163 | 208 |
| 158 | 210 |
| 157 | 210 |
| 158 | 210 |
| 157 | 210 |
| 170 | 198 |
| 167 | 180 |
| 160 | 187 |
| 167 | 180 |
| 160 | 187 |
| 170 | 198 |
| 160 | 167 |
| 165 | 190 |
| 162 | 175 |
| 166 | 200 |
| 169 | 179 |
| 159 | 217 |
| 162 | 175 |
| 166 | 200 |
首先介绍一些基本的统计函数:
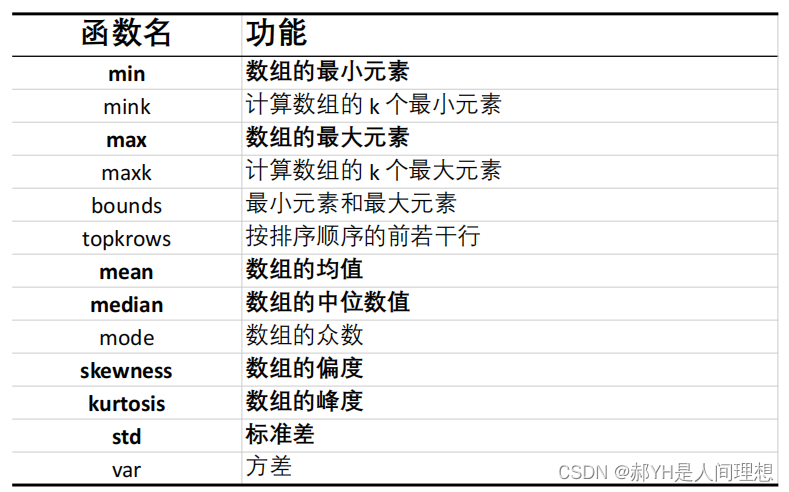
如下是计算皮尔逊相关系数的代码:
x=[163,158,157,158,157,170,167,160,167,160,170,160,165,162,166,169,159,162,166];y=[208,210,210,210,210,198,180,187,180,187,198,167,190,175,200,179,217,175,200];R=corrcoef(x,y);如下代码会返回假设检验要用到的p值:
[R,P]=corrcoef(x,y);如下是正态分布检验用到的代码:
%% 正态分布检验[hx,px] = jbtest(x,0.05);[hy,py] = jbtest(y,0.05);disp(H)disp(P)如下是计算斯皮尔曼相关系数的代码(通常情况下两种相关系数不一样大):
(注意:x与y必须是列向量)
Rs=corr(x',y','type','Spearman');斯皮尔曼相关系数假设检验的公式:
test=(1-normcdf(Rs*(19-1)^1/2))*2;test值>0.05即无法拒绝原假设。
如上即为操作的基本功。
五.其他有关的一些列技巧
相关技术等统计学问题,用SPSS计算往往更方便,如下图:

勾选自己想要的选项:
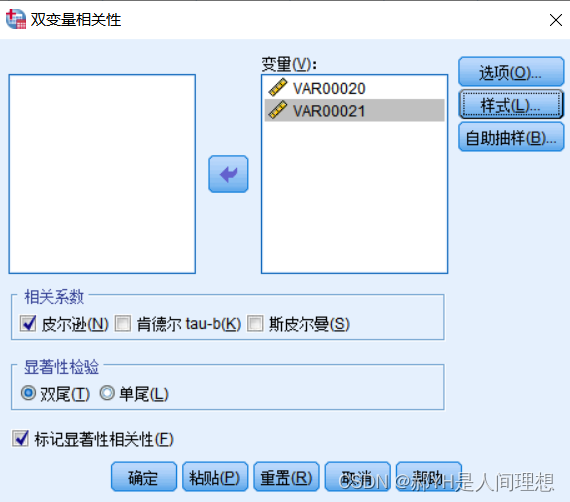
计算结果如下:
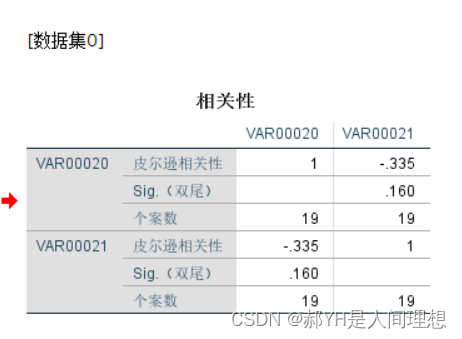
此外,关于热力图的画法,MATLAB种用到函数heatmap(R),其中R即为相关系数矩阵。
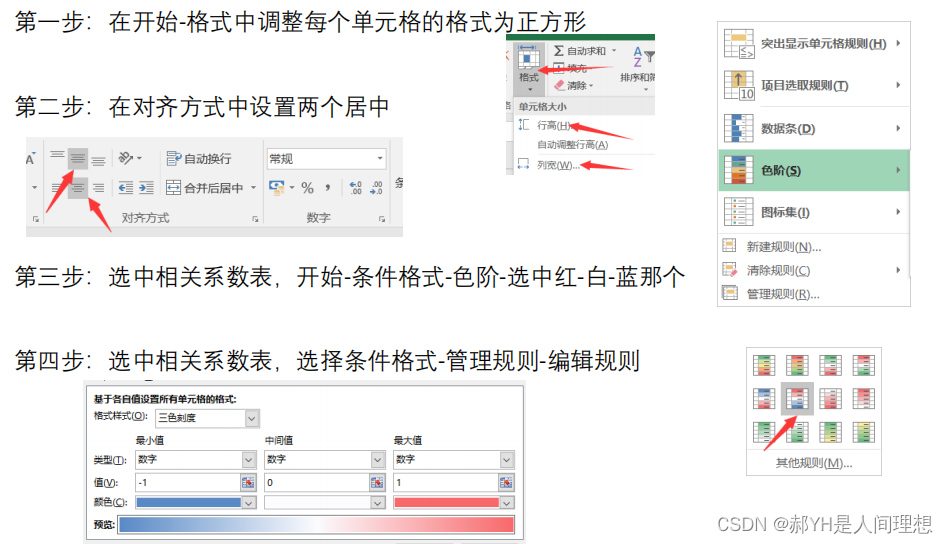
此处介绍一种更投机的操作方式——Excel法:

具体的方式就是,把相关系数矩阵沾进Excel中,再将行列大小调成一致——成正方形显示~再根据条件格式设置样式~
六.案例展示
分享在数模和市场调研大赛中用到相关性分析的典例:

 21年亚太赛的案例,当时第一次纯小白,画得属实抽象.........
21年亚太赛的案例,当时第一次纯小白,画得属实抽象.........
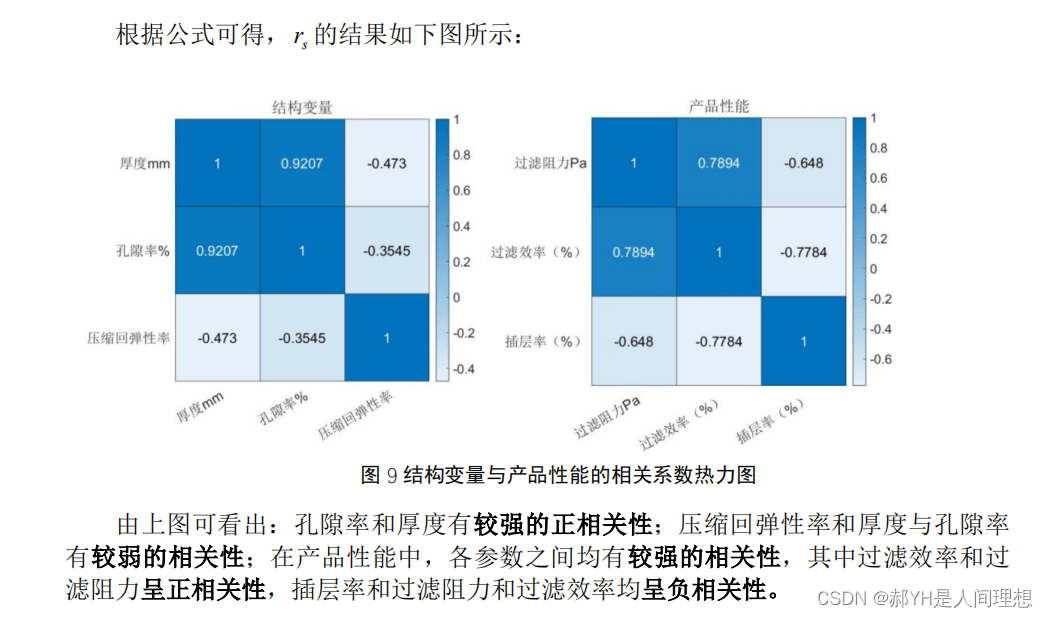 22年华数杯,有进步
22年华数杯,有进步
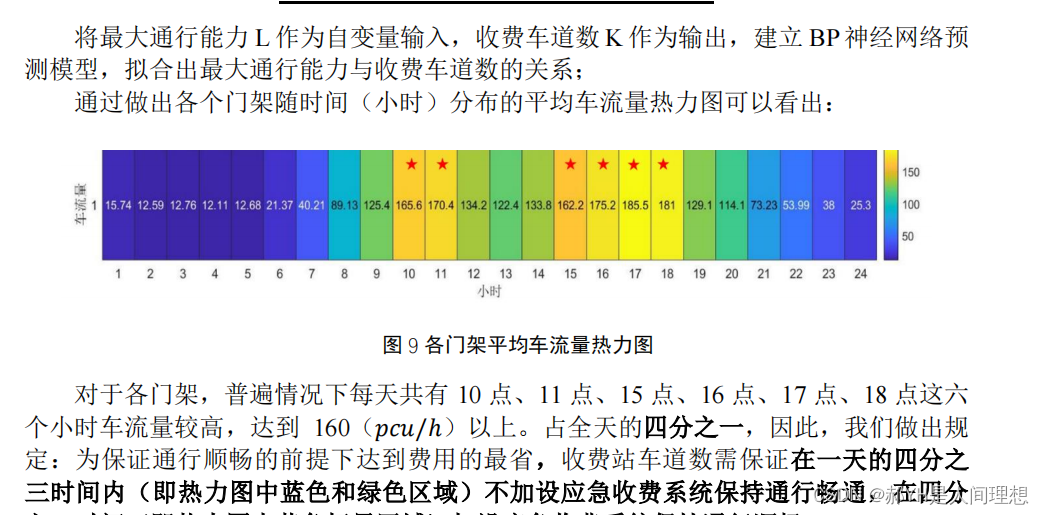
22国赛选拔赛,渐入佳境
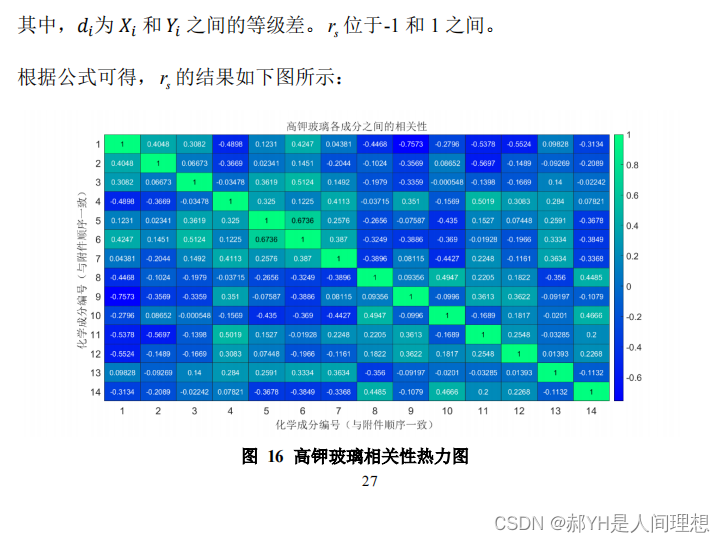
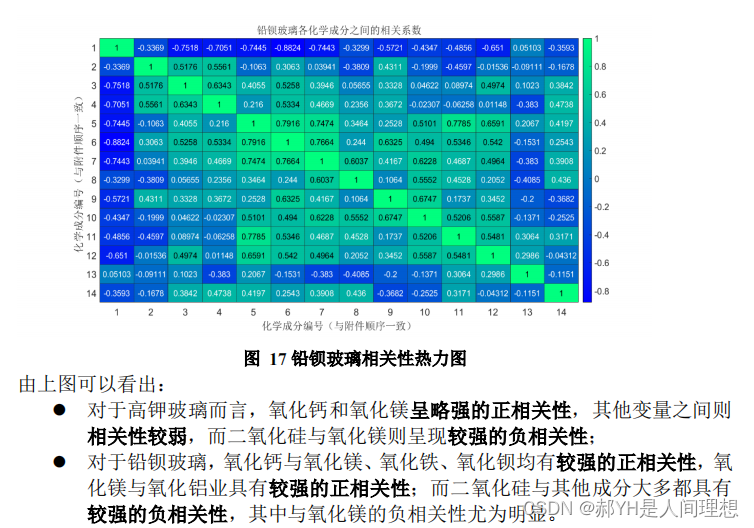
22年国赛,养兵千日用兵一时(写得有点问题,不重要。。。当时已经交了才发现错误)
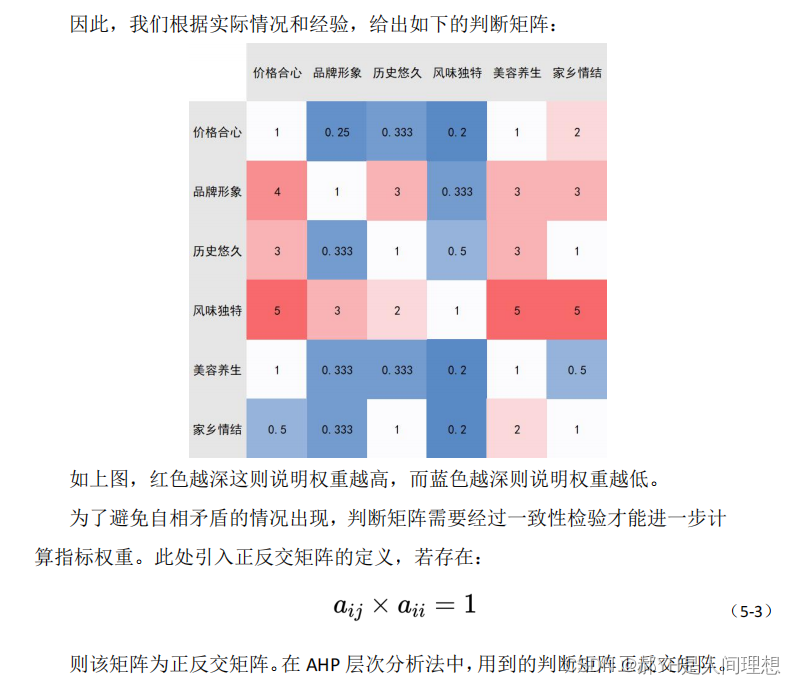
23年正大杯——这种就是前文提到的Excel法,属实有点low哈哈哈,平时小打小闹无所谓,学术论文尽量还是正经画比较好~
七.实战操作
来做一个实战:很多小伙伴都会关心——考研时名校会不会对本科出身比较有成见呢?我们采用23年WHU电子信息专硕的录取情况来做一个统计~
我们计算4组相关系数:
初试成绩与本科出身复试成绩与本科出身初试成绩与录取情况出生与录取情况其中,我们对本科出身做出如下正向化——即学校越好得分得分越高:
| 学校类型 | 对应数值 |
| 武汉985 | 4 |
| 其他区域985 | 3 |
| 211 | 2 |
| 双非及以下 | 1 |
而是否拟录取使用1和0分别标记。
注意:实际上,处理0-1变量,更适合使用Logistic回归,不过这里为了说明相关性分析的主要思想就凑合用了...
最后得到如下118条数据:
| 序号 | 初试得分 | 复试得分 | 出身 | 录取情况 |
| 1 | 428 | 88.72 | 4 | 1 |
| 2 | 414 | 89.04 | 3 | 1 |
| 3 | 423 | 86.12 | 3 | 1 |
| 4 | 405 | 91.08 | 2 | 1 |
| 5 | 396 | 91.28 | 4 | 1 |
| 6 | 412 | 86.12 | 2 | 1 |
| 7 | 401 | 89.32 | 1 | 1 |
| 8 | 402 | 88.88 | 4 | 1 |
| 9 | 403 | 87.92 | 3 | 1 |
| 10 | 426 | 80.08 | 4 | 1 |
| 11 | 421 | 80.6 | 1 | 1 |
| 12 | 403 | 84.68 | 4 | 1 |
| 13 | 396 | 86.36 | 4 | 1 |
| 14 | 377 | 91.32 | 4 | 1 |
| 15 | 412 | 80.8 | 1 | 1 |
| 16 | 401 | 84 | 3 | 1 |
| 17 | 392 | 86 | 1 | 1 |
| 18 | 394 | 84.72 | 4 | 1 |
| 19 | 384 | 87.16 | 2 | 1 |
| 20 | 402 | 81.4 | 3 | 1 |
| 21 | 391 | 84.68 | 4 | 1 |
| 22 | 384 | 86.68 | 2 | 1 |
| 23 | 387 | 85.28 | 3 | 1 |
| 24 | 385 | 85.64 | 4 | 1 |
| 25 | 392 | 83.32 | 3 | 1 |
| 26 | 409 | 77.16 | 3 | 1 |
| 27 | 370 | 88.68 | 2 | 1 |
| 28 | 393 | 81.52 | 2 | 1 |
| 29 | 402 | 78.76 | 3 | 1 |
| 30 | 371 | 87.8 | 4 | 1 |
| 31 | 363 | 89.88 | 2 | 1 |
| 32 | 371 | 87.4 | 1 | 1 |
| 33 | 363 | 89.64 | 4 | 1 |
| 34 | 356 | 91.64 | 1 | 1 |
| 35 | 370 | 87.36 | 2 | 1 |
| 36 | 361 | 89.72 | 4 | 1 |
| 37 | 394 | 79.76 | 1 | 1 |
| 38 | 374 | 85.48 | 2 | 1 |
| 39 | 377 | 84.36 | 1 | 1 |
| 40 | 360 | 89.4 | 2 | 1 |
| 41 | 380 | 83.36 | 2 | 1 |
| 42 | 377 | 84.24 | 2 | 1 |
| 43 | 388 | 80.92 | 3 | 1 |
| 44 | 360 | 89.32 | 3 | 1 |
| 45 | 389 | 80.44 | 2 | 1 |
| 46 | 364 | 87.88 | 4 | 1 |
| 47 | 368 | 86.04 | 1 | 1 |
| 48 | 388 | 79.84 | 2 | 1 |
| 49 | 356 | 89.4 | 4 | 1 |
| 50 | 381 | 81.8 | 3 | 1 |
| 51 | 374 | 83.36 | 3 | 1 |
| 52 | 371 | 84.2 | 4 | 1 |
| 53 | 383 | 80.6 | 1 | 1 |
| 54 | 369 | 84.76 | 1 | 1 |
| 55 | 367 | 85.32 | 2 | 1 |
| 56 | 386 | 79.4 | 4 | 1 |
| 57 | 377 | 81.48 | 3 | 1 |
| 58 | 359 | 86.88 | 1 | 1 |
| 59 | 376 | 81.64 | 2 | 1 |
| 60 | 371 | 83.12 | 4 | 1 |
| 61 | 376 | 81.32 | 3 | 1 |
| 62 | 375 | 81.6 | 1 | 1 |
| 63 | 355 | 87.48 | 1 | 1 |
| 64 | 375 | 81.24 | 3 | 1 |
| 65 | 361 | 85.32 | 3 | 1 |
| 66 | 361 | 85.04 | 2 | 1 |
| 67 | 369 | 82.6 | 3 | 1 |
| 68 | 365 | 83.64 | 2 | 1 |
| 69 | 358 | 85.56 | 1 | 1 |
| 70 | 369 | 81.8 | 2 | 1 |
| 71 | 372 | 80.88 | 3 | 1 |
| 72 | 364 | 83.24 | 1 | 1 |
| 73 | 365 | 82.68 | 1 | 1 |
| 74 | 366 | 82.36 | 2 | 1 |
| 75 | 359 | 84.12 | 2 | 1 |
| 76 | 372 | 80.12 | 4 | 1 |
| 77 | 365 | 81.96 | 4 | 1 |
| 78 | 359 | 83.72 | 1 | 1 |
| 79 | 357 | 84.2 | 1 | 1 |
| 80 | 363 | 81.72 | 1 | 1 |
| 81 | 366 | 80.56 | 2 | 1 |
| 82 | 355 | 83.64 | 1 | 1 |
| 83 | 356 | 83.32 | 2 | 1 |
| 84 | 383 | 75.08 | 2 | 1 |
| 85 | 373 | 78.04 | 1 | 1 |
| 86 | 372 | 78.32 | 2 | 1 |
| 87 | 360 | 81.88 | 2 | 1 |
| 88 | 385 | 74.28 | 4 | 0 |
| 89 | 357 | 81.92 | 2 | 0 |
| 90 | 392 | 71.4 | 2 | 0 |
| 91 | 365 | 79.12 | 1 | 0 |
| 92 | 361 | 79.48 | 2 | 0 |
| 93 | 378 | 74.2 | 1 | 0 |
| 94 | 380 | 73.28 | 1 | 0 |
| 95 | 370 | 76.16 | 3 | 0 |
| 96 | 359 | 79.4 | 1 | 0 |
| 97 | 371 | 75.44 | 4 | 0 |
| 98 | 359 | 78.32 | 1 | 0 |
| 99 | 367 | 75.68 | 2 | 0 |
| 100 | 357 | 78.2 | 4 | 0 |
| 101 | 361 | 76.48 | 1 | 0 |
| 102 | 362 | 75.6 | 1 | 0 |
| 103 | 394 | 65.56 | 2 | 0 |
| 104 | 394 | 65.52 | 1 | 0 |
| 105 | 387 | 67.56 | 1 | 0 |
| 106 | 377 | 70.16 | 2 | 0 |
| 107 | 370 | 71.8 | 2 | 0 |
| 108 | 359 | 74.8 | 1 | 0 |
| 109 | 361 | 73.56 | 2 | 0 |
| 110 | 362 | 73.2 | 2 | 0 |
| 111 | 358 | 73.96 | 1 | 0 |
| 112 | 358 | 73.88 | 2 | 0 |
| 113 | 355 | 74.4 | 2 | 0 |
| 114 | 368 | 69.32 | 2 | 0 |
| 115 | 355 | 71.96 | 3 | 0 |
| 116 | 356 | 70.88 | 1 | 0 |
| 117 | 367 | 61.52 | 1 | 0 |
| 118 | 360 | 63.08 | 1 | 0 |
直接用MATLAB一个corrcoef搞定,结果如下:
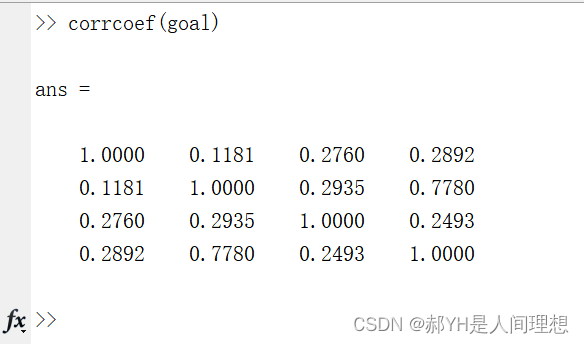
因此得出如下相关系数的结果:
初试成绩与本科出身:0.2760复试成绩与本科出身:0.2935初试成绩与录取情况:0.2892出生与录取情况:0.2493综上,我们可以得出结论:
首先,初试成绩与本科出身的相关性较低,这现实逻辑相一致——初试成绩仅与过去一年你的投入时间成本呈强烈正相关,而与别的面板数据——比如绩点等,没有太大的关系;
此外,复试成绩与本科出身并没有很强的相关性,证明该校不歧视本科出身;
初试成绩与录取情况虽然成较弱的正相关,可能有两个原因——一是模型的严谨性不足,另一方面可能是因为初试成绩占比相对较低(巧合的是复试强相关......),这要不同学校具体分析;
最后,出身与录取情况呈弱相关,说明上岸与否,全掌握在自己手里。
天助自助者,望诸君共勉~