专栏导读
作者简介:工学博士,高级工程师,专注于工业软件算法研究本文已收录于专栏:《复杂函数拟合案例分享》本专栏旨在提供 1.以案例的形式讲解各类复杂函数拟合的程序实现方法,并提供所有案例完整源码;2.复杂函数包含:分段函数、积分函数、常/偏微分函数、隐函数、方程组、级数函数、多参数函数;3.拟合工具是Matlab种的lsqcurvefit, nlinfit,神经网络,ga遗传算法,MultiStart全局优化算法等;4.拟合案例均源自科研实践中遇到的案例,文本教程+视频教程+案例源码,三向强化学习!提高大家解决实际数学建模的问题。【案例源码地址】Matlab实现分段函数拟合(分段点未知)| 源码分享 | 视频教程【视频课程地址】Matlab复杂函数非线性拟合专题/lsqcurvefit/nlinfit/积分函数、微分函数、隐函数、方程组、最小二乘法/机器学习/神经网络/编程/人工智能_哔哩哔哩_bilibili,欢迎订阅专栏,订阅用户可私聊进入Matlab编程交流群(知识交流、问题解答),并获赠丰厚的Matlab相关学习资料(教材、源码、视频课)专栏订阅地址:https://blog.csdn.net/u010542847/category_12576325.html文章目录
专栏导读
文章目录
案例介绍:
另外,再提供一种matlab表示分段函数的方法:piecewise函数
拟合经验:
1. 数据预处理
2. 确定分段数目
3. 选择合适的分段模型
4. 考虑分段连接处的平滑性和连续性
5. 参数优化和调整
复杂函数拟合的学习资料
案例介绍:
本案是针对一个分段函数中的参数进行拟合,使用的拟合工具是matlab中的lsqcurvefit或nlinfit。函数形式和待拟合参数如下所示。该案例的特殊之处在于分段点也是待拟合参数,因此如何自定义拟合函数,实现分段点的拟合是本案例最大的难点。本案例提供了三种分段函数的拟合方法:1.是用if……else条件语句定义的分段函数;2.另一种是通过(x0>a1)*f1+(x0<=a1)*f2这种形式定义的分段函数;3.第三种是通过sub1=find(x0<=a1);X1=x0(sub1);y(sub1)=f1;sub2=find(x0>a1);X2=x0(sub2);y(sub2)=f2实现分段函数的定义。三种方法原则上都没有错误,但是拟合的效果各有差别,最终我们选取拟合效果最好的第三种方法。

要求:各参数在规范中取值如下表,拟合出的参数值尽量和规范的参数值不要相差太多。
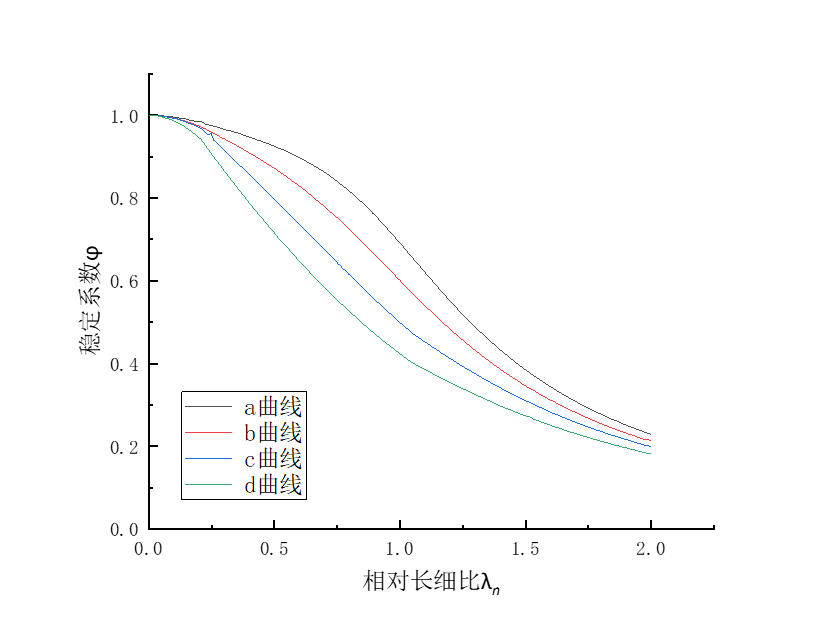
| 曲线类型 | 失稳方向 | α1 | α2 | α3 | λn,0 | 备注 |
| 规范曲线 | 强轴 | 0.650 | 0.965 | 0.300 | 0.215 | — |
| 弱轴 | 0.730 | 0.906 | 0.595 | 0.215 | λn,0≤1.05 | |
| 1.216 | 0.302 | 0.215 | λn,0>1.05 | |||
| 更新曲线 | 强轴 |
|
|
|
|
|
| 弱轴 |
|
|
|
|
|
规范曲线如下图所示,做出的曲线符合下图的趋势,分段点出尽量保持平滑。
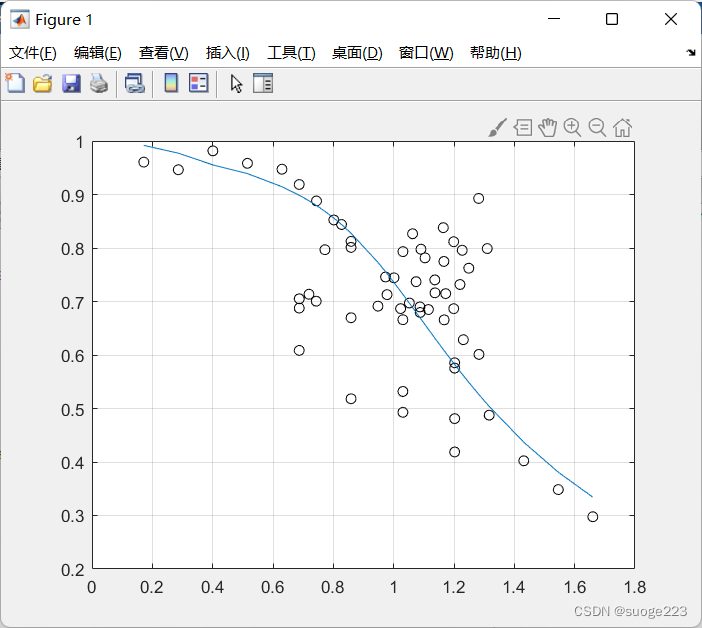
最终我们的拟合效果如下,可见整体分段点处还是比较平滑的
另外,再提供一种matlab表示分段函数的方法:piecewise函数
MATLAB 中的符号计算工具箱(Symbolic Math Toolbox)可以使用符号表达式来表示分段函数。通过符号表达式,可以直接定义分段函数的表达式和条件。
syms x;piecewise_expr = piecewise(x < 0, x^2, x >= 0 & x < 1, x, x >= 1, exp(x));MATLAB 中的匿名函数也可以用来表示分段函数。通过匿名函数,可以直接定义分段函数的表达式,并在需要时调用。
piecewise_function = @(x) piecewise(x < 0, x^2, x >= 0 & x < 1, x, x >= 1, exp(x));利用上述piecewise理论上也可以实现自定义分段函数,从而实现分段函数的拟合。
拟合经验:
分段函数的拟合是在给定数据集的情况下,尝试找到最佳的分段函数,以最好地拟合数据。以下是一些分段函数拟合的经验:
1. 数据预处理
在进行分段函数拟合之前,首先需要对数据进行预处理。这包括数据清洗、去除异常值、归一化等操作,以确保数据的质量和一致性。
2. 确定分段数目
在进行分段函数拟合时,需要事先确定分段数目。分段数目的选择可以根据实际情况和拟合要求进行调整。通常情况下,分段数目越多,模型越复杂,拟合精度越高,但也会增加过拟合的风险。
3. 选择合适的分段模型
根据数据的特点和拟合要求,选择合适的分段模型。常见的分段模型包括分段线性函数、分段多项式函数、分段常数函数等。在选择分段模型时,需要考虑模型的灵活性、拟合精度和计算复杂度等因素。
4. 考虑分段连接处的平滑性和连续性
在拟合分段函数时,需要特别注意分段连接处的平滑性和连续性。可以通过添加约束条件或优化算法来调整分段连接处的平滑性,以确保拟合结果的连续性和稳定性。
5. 参数优化和调整
在拟合分段函数时,通常需要对分段函数的参数进行优化和调整,以最小化拟合误差。可以使用最小二乘法、梯度下降法等优化算法来优化参数,以获得最佳的拟合效果,可通过调整lsqcurvefit, nlinfit中的初始值来提高拟合效果。
复杂函数拟合的学习资料
b站和仿真秀推出了一套通用的复杂函数拟合专题课程,包含了各类函数的拟合和一些共性问题的解决处理。拟合工具是lsqcurvefit, nlinfit,神经网络工具箱。复杂函数拟合包括积分函数、微分方程、偏微分函数、隐函数、方程组的拟合,其中积分函数的拟合又包括被积函数存在待定参数和积分上下限存在待定参数两大类。这些拟合问题均源自实际科研过程中遇到的案例,并且均为非常规拟合问题,现有网络资源几乎找不到类似案例。
【Matlab复杂函数非线性拟合专题/lsqcurvefit/nlinfit/积分函数、微分函数、隐函数、方程组、最小二乘法/机器学习/神经网络/编程/人工智能-哔哩哔哩】 https://b23.tv/iFy1cKt
Matlab复杂函数拟合专题课13讲,附赠所有案例的matlab源码和数据文件_非线性_通用_MATLAB_参数优化_试验-仿真秀视频课程

提示:以下是本篇文章正文内容,下面案例可供参考