张士玉小黑屋

   最近，全世界燃起一股围剿ChatGPT的势头。由马斯克、图灵奖得主Bengio等千人联名的“暂停高级AI研发”的公开信，目前签名数量已上升至9000多人。除了业内大佬，欧盟各国和白宫也纷纷出手。   最早“动手”的是意大利，直接在全国上下封禁了ChatGPT，只给OpenAI20天的调整适应期，若拿不出合格的方案就得交最高2000万欧元的罚款。   随后，加拿大隐私专员办公室（OPC）宣布开始调查ChatGPT背后的公司OpenAI；德国联邦数据保护专员发言人称禁止ChatGPT的使用是可能的；法国、爱尔兰、西班牙和瑞典等国家也开始考虑对人工智能(AI)采取更严格的监管。    不仅如此，多国企业和机构也开始调查或采取措施限制使用该软件。3月末，韩国三星半导体部门发生了3起

圆形识别（圆检测）是图像识别中很常见的一种处理方式，最核心的是cv2.HoughCircles这个函数实现的圆形检测。当然还有一些其他的处理过程，以下详述：1读入图像首先需要读取一个图像文件，将其作为一个变量img=cv2.imread("save1.jpg",0)#0或者cv2.IMREAD_GRAYSCALE读取为灰度图像img2=cv2.imread("save1.jpg",1)#1或者cv2.IMREAD_COLOR读取为为彩色图像img是一个ndarray，2维结构，包含的是灰度化后的图像信息img2是一个ndarray，3维结构，包含的是RGB彩色图像信息，比img2多出一个色彩维度如下图，img2是3个方括号“[”2图

2021年第八届大唐杯全国大学生移动通信5G技术大赛省赛实验背景、勘站规划、网络部署、开通调测、业务认证摘自：https://www.bilibili.com/video/BV1Hr4y1Y7m8?spm_id_from=333.337.search-card.all.click车联网部分摘自：https://www.bilibili.com/video/BV1Pu411v7gE?spm_id_from=333.337.search-card.all.click感谢up主倾情相授。1、实验背景2、勘站规划2.1射频规划2.2天线挂高2.3下倾角2.4设备选型2.5光纤2.6光模块2.7电源类型3、网络部署3.1OMC机柜参数3.1.1传输参数

这一篇能节省你在 kubeadminit时遇到问题的排错时间⌚️。整合了网上大佬的方案?‍♂️和官方建议⚠️。个人被这个问题折磨了好久?，希望总结出来能帮助到大家～目录自定义配置文件初始化的建议关注配置： advertiseAddressimageRepositorynodeRegistration.criSocket         解决：thisversionofkubeadmonlysupportsdeployingclusterswiththecontrolplaneversion>=1.26.3.Currentversion:v1.22解决：failedtopullimageregi

?博主简介  ?云计算领域优质创作者  ?华为云开发者社区专家博主  ?阿里云开发者社区专家博主?交流社区：运维交流社区欢迎大家的加入！文章目录报错详情解决方式1、下载metrics-server-components.yaml2、将metrics-server-components.yaml中的k8s.gcr.io更改为阿里云镜像地址3、执行metrics-server-components.yaml4、查看pod

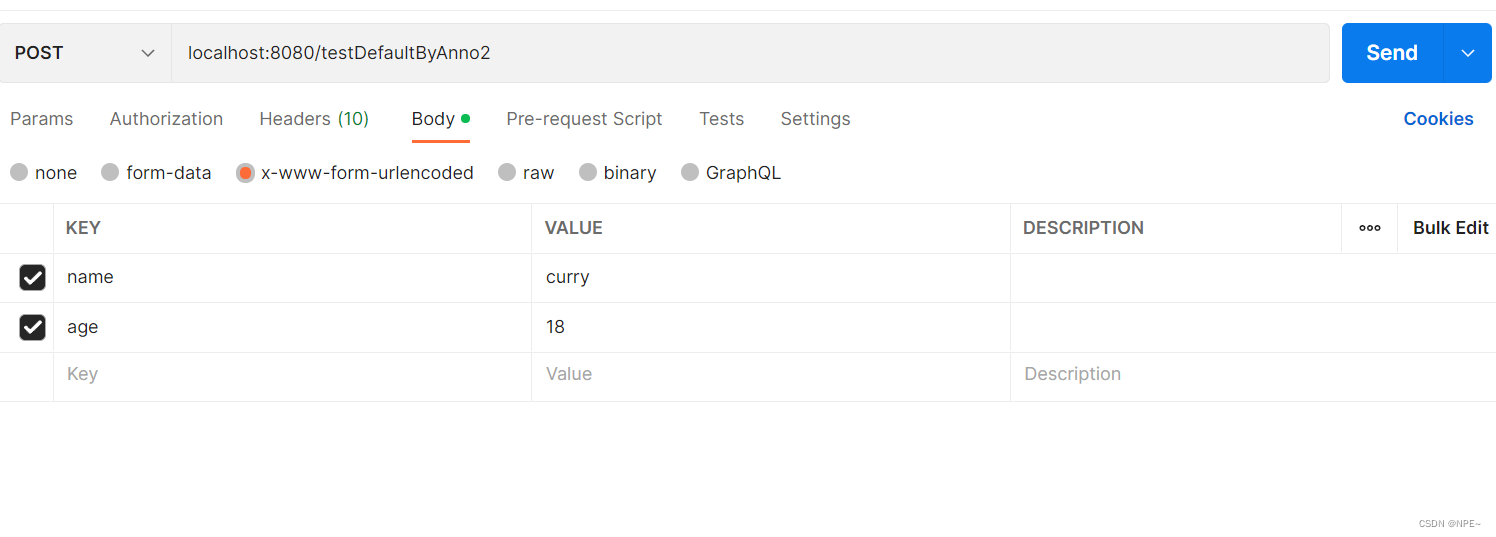
前端与后端传递数据——JSON1前端传送JSON数据给后端1.1application/x-www-form-urlencoded默认格式1.1.1通过HttpServletRequest获取数据/***通过request获取数据*@paramrequest*@return*/@PostMapping("/testDefaultWithNoAnno1")publicStringtestDefaultWithNoAnno1(HttpServletRequestrequest){Stringname=request.getParameter("name");System.out.println("str>&g

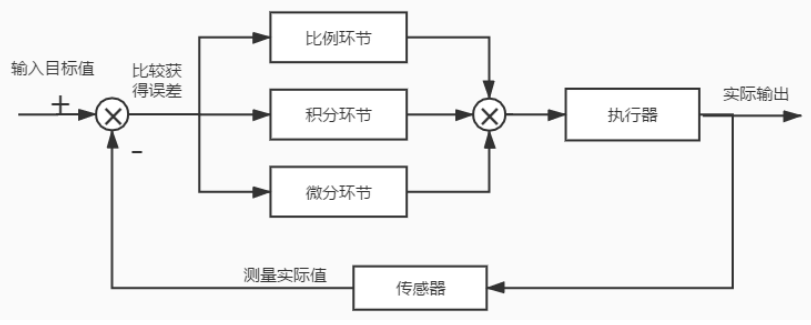
PID算法介绍PID是Proportional（比例）、Integral（积分）、Differential（微分）的首字母缩写；是一种结合比例、积分和微分三种环节于一体的闭环控制算法。PID控制的实质是对目标值和实际值误差进行比例、积分、微分运算后的结果用来作用在输出上。比例（P）比例控制是最简单的一种控制方式，成比例的反应控制系统中输入与输出的偏差信号，只要偏差一旦产生，就立即产生控制的作用来减小产生的误差。比例控制器的输出与输入成正比关系，能够迅速的反应偏差，偏差减小的速度取决于比例系数Kp,Kp越大偏差减小的就越快，但是极易引起震荡；Kp减小发生震荡的可能性减小，但是调节的速度变慢，单纯的比例控制存在不能消除的静态误差，这里就需要积分来控制。积分（I）在比例控制环节

1.初始化列表：1.1为什么要有初始化列表？实验代码如下：classA{public:int_a1;//声明int_a2;constint_x;};intmain(){Aaa;//定义return0;}?运行结果：❓有一个const成员函数时，定义对象会报错?原因：const变量必须在定义的地方初始化❓对象在main函数内定义，而对象中的成员变量在哪里初始化呢？?可以使用缺省值constint_x=1;//缺省值，可以过因此我们需要考虑有const的情况，我们要想办法初始化成员变量1.2初始化列表的写法：初始化列表：以一个冒号开始，接着是一个以逗号分隔的数据成员列表，每个"成员变量"后面

 大家好，我是爱分享的小蓝，欢迎交流指正~ 全文目录??说在前面?模板-BFS迷宫⭐?传送锚点​ ?思路点拨?代码详解  ?走迷宫Ⅰ⭐?传送锚点 ?思路点拨?代码详解  ?走迷宫Ⅱ⭐?传送锚点 ?思路点拨?代码详解  ?走迷宫Ⅲ⭐?传送锚点 ?思路点拨?代码详解   ?扩散⭐⭐?传送锚点 ?思路点拨?代码详解   ?全球变暖⭐⭐⭐?传送锚点​ ?思路点拨?代码详解 ?说在前面鸽了一个星期的BFS模板，小蓝肝了10小时终于写完啦！q(≧▽≦q)看了十几份题解，调试了上百次程序，终于把原本四十行的代码，精简压缩成20行模板\^o^/但小蓝调试的时候，出现好多BUG，研究了几个小时才找到错误原因解决(ToT)/~~~如果没有人指导的

目录哈夫曼树树的带权路径长度(wpl)哈夫曼编码代码实现哈夫曼树封装哈夫曼树的节点构建哈夫曼树字典树执行流程代码实现字典树封装字典树的节点构建字典树哈夫曼树       哈夫曼树（HuffmanTree）是一种带权路径长度最短的二叉树。哈夫曼树常常用于数据压缩，其压缩效率比较高。哈夫曼树的构建过程主要有两个步骤：（1）选取权值最小的两个节点构造新的二叉树，其权值为两个节点权值之和；（2）将新生成的节点加入到原来的节点集合中，重复执行步骤一和步骤二，直到只剩下一个节点，这个节点就是哈夫曼树的根节点。哈夫曼树的构建过程可以用贪心算法实现，构建出的哈夫曼树可以保证带权路径长度最短。树的带权路径长度(wpl)        树的带权路径长度（weightedp